
Deleuze of The Logic of Sense places ‘problems’ at the very base of his entire ontology. To put it (overly) simply, problems are what constitute the most basic strata of reality. Problems work as jets of ‘singularities’ which, when minimally registered in the order of language, are ‘events’; the events engender things and their shifting properties, and propositions, subjects, knowledge, and all the rest. Problems, singularities, events, sense, come first, then things, words, knowledge, subjects. A true reversal of Platonism. Thus, the notion of the problem, and the singularity, are indispensable in coming to grips with Deleuze’s pre-Guattari philosophy (and arguably the latter as well).
“We can speak of events only in the context of the problem whose conditions they determine. We can speak of events only as singularities deployed in a problematic field, in the vicinity of which the solutions are organized” (Deleuze, 1990, p.56)
This is characteristically opaque. Bowden (2011) and Voss (2013) have made admirable attempts to provide brief formulations of what Deleuze means by ‘problem’:
“Deleuze speaks of the problem as the reciprocal, complete and progressive determination of purely ‘differential elements’ by means of the ‘adjunction’ and ‘transformation’ of singularities-events, where singularities-events are understood to correspond to the ‘values’ of relations between differential elements, and where differential elements are in turn determined by syntheses of singularities-events.” (Bowden, 2011, p.98)
“For Deleuze, the ‘problem’ is thus a differential structure endowed with an intrinsic genetic power to generate sense. Although the problem can be incarnated in propositional form and in the empirical world, it belongs to an extra-propositional and sub-representative realm.” (Voss, 2013, p.11)
However, this will all obviously require some extensive unpacking.
To begin, Smith (2006) describes how Deleuze, following Proclus, interprets the history of mathematics as a tension between problematics and axiomatics. More particularly, the interpretation of mathematical objects inherent in each pole. In axiomatics we deduce the consequences of axioms and definitions — finding logical entailments in an analytic process. Euclid’s elements is the premier example of this. In problematics, we are given problems of the sort “Using only a compass and straightedge, construct an equilateral triangle”. The ‘solutions’ to such problems are necessarily procedural, not in a deductive way through steps of a rational proof with analytic connections between each step (which are fundamentally atemporal), but in an algorithmic way where we must first create other shapes, two circles for example, and then orient by their relations and intersections. All ‘quantities’ here are strictly relative to each other; we don’t decompose the problem onto an absolute grid (number lines or cartesian coordinate system) in order to translate from one function to another through an ‘overarching’ layer not native to the terms of the problem itself, but rather specify a number of steps, a number of transformations, in the figures themselves.
Famously, one of these problems, the finding of a square equal to the area of a given circle, went unsolved for millennia (before it was proven, axiomatically, to be unsolvable). In fact, this problem can demonstrate nicely the difference: we can just state that it is the square whose edges are constructed from line segments each the square root of the area of the circle. Thus, we give the function of the translation from one figure to another, stating the rule of their identity. However, the problem still stands on its own terms. The ‘square root’ solution translates the problem into a more manageable space, governed by axioms and arithmetic operations. The “using only a compass and straightedge” should not be seen as an arbitrary limitation, to make a recreational game out of problems that are much more easily solved using arithmetic, axiomatic methods, but taken quite literally as essential to the problem itself. Knowing I can create circles and lines of any given magnitude, and specify the precise point that form the centers of these circles, thus am able to divide circles into quadrants, and construct all manner of triangles and other figures whose areas share relationships with the figures from which they are formed or drawn in relation to, then, from an limitless series of ideal constructions, it seems possible that I could be able to ‘square the circle’. The problem does not ask for a magnitude, but a series of ideal events that produce a progressive, reciprocal structure defining the transformation, with full access to the elements from which these forms are composed (line segments and circles).
Smith continues that this tension within mathematics, between problematics which have not received an axiomatic formulation, and the more formalized, ‘venerable’, axiomatics is the dynamism that drives mathematical development:
“according to Deleuze, mathematics is constantly producing notions that have an objectively problematic status; the role of axiomatics (or its precursors) is to codify and solidify these problematic notions, providing them with a theorematic ground or rigorous foundation.” (Smith, 2006, p.156)
“In Deleuzian terms, one might say that while ‘progress’ can be made at the level of theorematics and axiomatics, all ‘becoming’ occurs at the level of problematics.” (Ibid, p.158)
For example, ‘The Bridges of Königsberg’ is one such ‘problematic’ problem: given a (specified) number of bridges across a (specified) number of islands, is it possible to cross every bridge on a single path once and only once? Smith’s point here is borne out by Euler, who in solving the problem (it’s not possible) on the one hand develops a new branch of mathematics (graph theory) while on the other doubting whether this problem has anything to do with mathematics. From Euler’s letters we read:
“A problem was proposed to me about an island in the city of Königsberg, surrounded by a river spanned by seven bridges, and I was asked whether someone could traverse the separate bridges in a connected walk in such a way that each bridge is crossed only once. … This question is so banal, but seemed to me worthy of attention in that neither geometry, nor algebra, nor even the art of counting was sufficient to solve it.” (in Sachs, et al, 1988, p.136)
And in another letter:
“Thus you see … how this type of solution bears little relationship to mathematics, and I do not understand why you expect a mathematician to produce it, rather than anyone else, for the solution is based on reason alone, and its discovery does not depend on any mathematical principle.” (ibid.)
This is precisely Deleuze’s point in prioritizing the objects of ‘problematics’; the ambiguity as to their domain. The mathematician, here Euler, grasps the same problem as a tourist in Königsberg looking over a map in their hotel room planning the next day’s sightseeing. A problem stretches over these different registers and persists despite its solution. One could tell the tourist that Euler has proven that it cannot be done, but if one puts themselves in their shoes, one can palpably feel the semi-resigned “Yes, well, nevertheless…”. This is because “the problem bears resemblance neither to the propositions which it subsumes under it, nor to the relations which it engenders in the proposition” (Deleuze, 1990, p.122). A problem exceeds its nominal solutions.
One of the difficulties when thinking of the status of ‘problems’ is that we are prone to see them as inhering within the subject, thus lacking in objectivity. We can say to the tourist that Euler has proven the fact of the matter, and insofar as they still stare at the map (“but, surely there is some way”) we are just dealing with the stubbornness of a desire that would wish this problem solvable, but insofar as it isn’t, this desire is best done away with, to affect a more upstanding and ‘objective’ disposition (facts don’t care about feelings, etc etc ad nauseum). We tend to look at problems in terms of requiring some proposition that could function as their absolute solution, and thus the problem is defined negatively, and deficiently. Negative in that it calls for its corresponding answer only, and deficient in that it is referred to a gap in the subject, whether it be epistemic (don’t know) or concerning their abilities or possibilities (can’t do). Deleuze likens this characterization to a “radio quiz” epistemology (Deleuze, 2011, p.188) where there are answers in reserve that perfectly settle each and every question. He is completely opposed to this sterile and reductive image of both thought and truth.
Deleuze wants to maintain the problematic structure of problems right down to the core of things. Ultimately, things themselves are provisional solutions to problems. This is to say that when we ‘grasp’ a problem, we are not butting our heads up against our own ignorance or lack of ability, but grasping something ‘out there’ in the world. (This notion of individuated beings being problems Deleuze borrows from Simondon).
To get at this idea of the ‘objectivity of problems conceived as such’ we need to examine the conceptual links between problems, events, singularities, and sense. The relation between problems and events has been hinted at above. The problem calls for a series of ideal events to be carried out; the problem concerns a series of events. These events in turn provide conditions to the problem as it is developed through them. So, in the example above of squaring the circle, we might first inscribe two circles with a line segment spanning their centre-points. Now the problem has been altered: where to go from here? How to transform this figure into the one that will show a harmonious relation between one of these circles (or a further circle?) and four equal line segments? Or, as we wander around Königsberg, each bridge we cross needs to be crossed off, one less possible move available to us, and a whole new starting point on the island we now find ourselves on. A new problem whose solvability is a product of the steps we have already taken. In this way, problems are not static, but ‘undergo’ the events that they themselves produce or specify (using only a compass and straight-edge…). We can say here that problems are progressively determined. Think here of how a growth of a tree runs along a maximization problem: how to maximize exposure to sun light. The tree’s growth traces its way through the shifting environment, but each moment of growth, occurring at ‘only just’ imperceptible (for us) scale of time is changing the very environment in which the sunlight is maximizable by hoisting the branches this way or that. It’s not that the tree is meditating on a strategy — it’s that the tree is, in a sense, this strategy (among others in response to other problems that make up its becoming), progressively determining the conditions of the problem that it is (the possible differential interconnections between cells, water, and sunlight), while producing its own milieu in the process (a ‘world’ composed of sunlight, air, water, dirt and growth).
So, problems are conditioned progressively and reciprocally by the events they engender. But in what sense are these ‘events’ the events we ordinarily refer to: the delivering of the mail, the melting of the arctic, the arrival of the train?

Deleuze on Events
Deleuze asks why every event seems to be “a kind of plague, war, wound, or death?” (Deleuze 1990, p.151). Of course, we could reply that it is only ‘noteworthy’ events that are of this type; if ‘events’ are to be a robust metaphysical category, we would also need to add events like “the sitting of the pencil sharpener in the closed drawer”. But this equivocation does not solve anything, it merely reintroduces the slipperiness of events. I.e., is it only to a human consciousness that the destruction of a building is significantly different from the standing of a building, whereas on the level of Being there is nothing but an indifferent rearrangement, as Sartre has proposed (cf. Sartre, 2008, p.32)? Such a conclusion would trap events within a transcendental consciousness — presenting a kind of arbitrary schematism — nothing really happens but for the language of an irreducible subject who would describe things differently over time. Deleuze bypasses this conclusion by distinguishing between the ordinary and the singular.
In mathematics, when describing a curve given by a function, we distinguish singular from ordinary points. Roughly, the ordinary points on a curve are those regions where, given the trajectory of the line, we can successfully predict its ‘future’ trajectory as a mere continuation, given by its slope. In other words, the part of the curve that is ‘straight’. The singular points, on the other hand, are those points on the curve where the line curves, thus, our ability to determine what the function will ‘spit out’ as we go along this curve is not merely a forward and backward projection of its previous slope. It’s where the line ‘misbehaves’. It’s the singular points, orbiting the ‘singularity’, that characterize the curve and the function that generates it. The singularity is what the line, in its curves, appears to ‘orbit’, ‘seek’ ‘bend’, ‘tend’ or ‘avoid’. It’s an ‘ideal’ object that allows us to give a qualitative characterization of the curve.
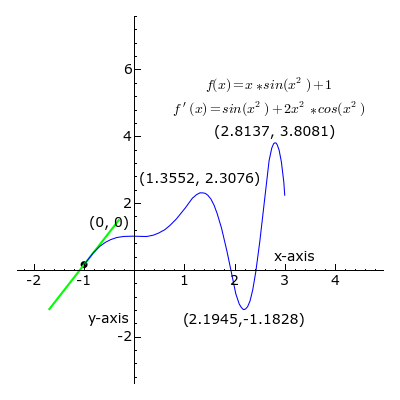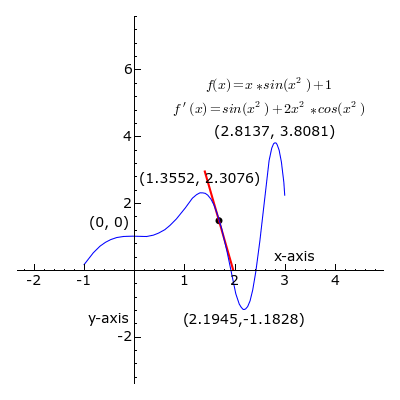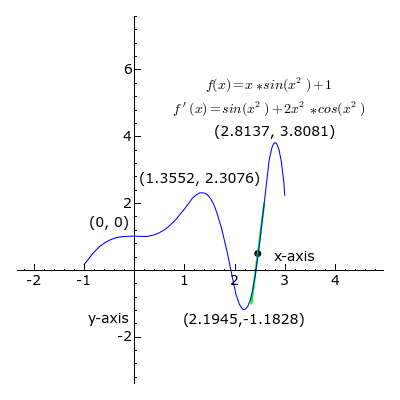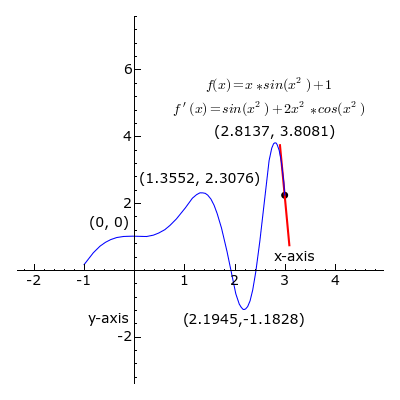
The ordinary points indicate a region of ‘meta-stability’ inherent in the function; when the value of x and y (or whatever values we are dealing with) sit within this range, we get an orderly progression that can be ‘compressed’ as a simple slope ratio. However, within that very same function, when this or that value is pressed beyond this range, quasi-unpredictability results; values get ‘stuck’, endlessly repeating themselves, or change in huge increments. Deleuze’s wager is that we can characterize those ‘noteworthy’ events (the ones we direct language at by discussing) as ‘singularities’, turning points, that represent the transition from one meta-stable, compressible progression to another. That is, singularities are points of mattering.
“What is an ideal event? It is a singularity — or rather a set of singularities or of singular points characterizing a mathematical curve, a physical state of affairs, a psychological and moral person. Singularities are turning points and points of inflection; bottlenecks, knots, foyers, and centers; points of fusion, condensation, and boiling; points of tears and joy, sickness and health, hope and anxiety, “sensitive” points. … [they are] essentially pre-individual, non-personal, and a-conceptual.” (Deleuze, 1990, p.52)
One useful thing about this approach is that all of the vicissitudes of the curve are immanent to the function that both engenders the ordinary and the singular — the curve does orbit a singularity, or reaches a ‘limit’, but neither singularity nor limit are external to the function. It’s not that the curve is circulating invisible objects on the plane, but rather these invisible objects are engendered by the behaviour of the curve as ideal or virtual loci — they’re a consequence of its extrapolation/realization in a ‘solution space’ (here, the graphing of the function as a curve). Furthermore, we shouldn’t think of either curve or function as primary. The ‘qualitative behaviour’ of the curve is merely a visualization of what is happening within the function — how the terms of it reciprocally condition each other by the rules of translation that the function describes. “The existence and distribution of singularities are relative to a problematic field defined by the equation as such” (Deleuze, 1990, p.54). However, conversely, when investigating a curve (an orbital trajectory for example) and establishing the function that seems to govern it, this function itself is merely a kind of description, a formalization. Thus, the relationship between problems (as functions) and events (singularities) should not be understood as one entity acting on another, as a ground to the grounded, but a reciprocal conditioning. A problem defines the ‘where’ and ‘when’ and even the ‘possibility’ of events, and the events in turn backwards condition the problem, clarifying it and the space that it defines. “It seems, therefore, that a problem always finds the solution it merits, according to the conditions which determine it as a problem” (ibid.) This becomes clearer when we think of how these ‘curves’, these singularities, play out in material events.

The Problem in Material Events
Take, for example, a pot of water slowly being heated. There is a huge number of dimensions we can select and pose in the form of the function (a ‘dimension’ here meaning any series we could plot on an axis). Heat and time, the dispersal of the water in space and the amount of tension at the surface, degrees of entropy, or even the likelihood of getting injured by sticking your hand into the pot. For a huge number of these dimensions that we can map, when the pot of water ‘boils’ (as, say, testified to by a visual series of perceptions — yet another dimension), all of them enter into a singularity, some more drastic than others, but all pointing to the transition from one meta-stable state to another, i.e., that something is happening. As the surface tension lowers, the probability of being injured by sticking your hand into the pot increases. At a certain point they both reach their limits, and the ordinary progression along a stable slope gives way to sharp curves. Visually, you can see the neighbourhood of the singularity, as a pot of bubbling water with steam rising up from it, with the visual series here being another dimension that reaches a singularity in the same neighbourhood as the others (‘seeing’ rapid and sudden changes). Not every dimension reaches its singular points at the precise moment the water reaches 100 degrees, but mapping enough of them we see they take that rough ‘region’ for their point of inflection, with the temperature series just being one dimension caught up in the singularity by its own progression (here reaching a limit at whatever the boiling point is). An event. And none of this is extrinsic to the little system we have created with the water in the pot on the stove — this singularity draws in these different dimensions with which we try to understand the system precisely because this water is like this, and this heat is like this, and this pot transfers heat like this because it is the way it is. And the reason these things are the way that they are is because of the singularities they have passed through in their particular formation, these events conditioning the problem that’s being determined right in front of us now. This repricocity is captured well in an example from Williams’ introduction to the Logic of Sense:
“Examples of events could be a set of animals altering course due to climatic change, … or the slow silting of a river strangling a port and its estuary into decay. In each of these cases there is a change that includes many continuing series of processes; the event has an impact thanks to its capacity to run along many different strands.
Neither an estuary nor a port are submissive recipients of changes in river flows, they exploit new opportunities and struggle against the silting of their ongoing life-forms, thereby implying different senses and values in the changes in flow.” (Williams, 2008, p.2–3)
But how to characterize the ‘problem’ in our example of the pot boiling? What’s the problem with the water? It’s simply that which I grasp at in thought when I wonder “when is this going to boil?”, or “will this burn me if I scoop my hand into it?” or any one of the other dimensions with which we could draw the curves that enter the singularity. That is, for us, as subjects, we ‘apprehend’ problems in the form of possible questions, in a manner akin to how Frege saw us ‘apprehending’ thoughts — as standing in a relation to something that pre-exists the individual and their apprehension. The switch is from positive propositions to questions themselves towards which these propositions would serve as more or less adequate responses. The intellectual act is the one of grasping that there exists some functional connection between two or more variables — some fateful conditioning, or tension. We stand on one of the ‘islands’ of Königsberg and we look at the bridges, and the grasping of the problem is the grasping of how all of the bridges are linked and related such that any action we take vis-à-vis one of them changes the relations. A ‘problem’ just is these set of transforming relations between series (or dimensions), a series of bridges and ‘islands’ and crossings, or anything else. The ‘grasping’ or ‘apprehending’ of a problem in the intellectual act of the formation of a question is just that familiar intellectual act: “What’s going on with this?”, “Surely this is possible…”, “What happens next?”, “When?”. We and our language and knowledge know this way of formulating thought as ‘questions’, but that which presses us to think, that which we try to formulate into a question, is the problem which has a certain indifference and ambivalent surpassing to the limited ways that we, at a given moment in history, have of formulating questions.
Again, this is not merely a contingently-universal human limitation “which would indicate only the imperfection of our method and the unhappy necessity for us not to know ahead of time — a necessity which would disappear as we acquire knowledge” (Deleuze, 1990, p.54), but, rather, that these questions (and their responses) gain their sense precisely insofar as they inquire into the dimensions across which the water is divided into terms of various functions (as descriptions) that tend towards singularities-events when differentially related. That is, a problem.
“Sense is thus expressed as the problem to which propositions correspond insofar as they indicate particular responses, signify instances of a general solution, and manifest subjective acts of resolution.” (Deleuze, 1990, p.121)
Accordingly, there is also a negative condition here too: those questions (along with their responses) are senseless that inquire after dimensions upon which no singularity occurs, but instead produce a line of ordinary points that stupidly progress ad infinitum.
In my reading here, the problem is the function that translates dimensions (or series) onto others. It is the ‘fact’ of their differential implication. We know they are connected (that there is a problem here) precisely because of the singularity-events they reciprocally engender/undergo at points on the series produced by their differential relation: in our example, boiling. This singularity appears in a curve we might want to draw on some note paper, where we extract two (or more) dimensions to act as terms of a function, but it also appears directly to us; as the empirical experience of a pot of water beginning to boil. I ask of the system “when will the water boil?” and this question has sense precisely in that it coordinates a series of times and series of states of the substance of water, producing a singularity. One method to answer this question, to ‘get at’ what it asks after, is to take some precise temperature measurements and estimate a curve, a rate of change and attempt to forward project where the singularity will occur. But another method to answer this question is to just wait and see. There, it’s boiling, so the answer is ‘now’. The pot itself is ‘processing’ the problem in its becoming, and in measuring and charting a curve we are merely translating that procedure of determination over into propositions, in line with a certain methodology and convention of formalization. The ‘problem’ (the function mapping these dimensions, along with myriad others, onto each other), as conditioned by an event (boiling), is progressively determined right there in empirical experience, and us having it. We could think of the amount of computing power we would need to predict the motions of a double pendulum, or we could just let a double pendulum do the calculations for us, by setting it in motion. In this way, the calculus and the trigonometry involved in motion is not some ‘secret’ behind the shuffling concatenation of objects, but is a useful manner for their description. The catcher in the field, ‘eyeballing’ the arc of the ball in order to catch it precisely at an anticipated point is grasping the same problematic that trigonometry articulates, just as Euler and the Königsbergians grasped the same problem of the ideal route across the bridges.

So, the conceptual edifice of problems-singularities-events-sense is a tangle of reciprocal conditionings. Our way of ‘getting at’ problems is through sense: we apprehend in thought a question asking after an event. An event is always a singularity, an ideal point in the progressive determination of a relation between two or more dimensions where the function begins to transition between meta-stable states. A resonance between series. Whether we grasp these problems or not, they are there, being ‘crunched’ all around us. Though a singularity-event appears across many different dimensions we may frame in thought, and infinitely many more than we commonly prioritize, not all dimensions become implicated to the same degree, thus not all propositions and questions are equal in sense. The cost of the water is somewhat perturbed by its boiling, but to trace a singularity we would need to situate this water in a more complex environment where such an ‘event’ could matter (i.e., a café, where the rate of water boiling might be tied in some way to profits — but note that this situation introduces new problematics, and re-conditions the problem from our previous example, and its precisely this new problematic field that now allows questions of the function between cost and boiling to produce sense).
A couple of caveats and elucidations are needful here. Firstly, in the above examples, I’ve used binary sets of series (time and state, heat and cost, etc), however, obviously when we are dealing with real things, they are never just a function of two series. We need to transition the image of two selected series that we are tracing the singularities of up to a n-dimensional space, where, despite how hard it is to visualize, singularities are still occurring because of the differential relations of these n-dimensions — an entire undulating manifold. The other caveat on the above examples is the selection of the series within or from the n-series. Here, our thought, when it achieves its positive expression is always beholden to a discursive sedimentation. There’s a pot of water, so it just seemingly ‘makes sense’ to ask of it when it will boil, which amounts to saying “let x be a series of times, and y a series of physical states, for what values of x and y does a singularity occur?” But we need to keep in mind that a) these are two series selected from an infinite possible number (all of which enter some singularity or another at a point we can translate across to coincide with the singularities within all the others), and b) these series themselves need to be specified and determined. ‘A series of times’ is not something given ready-made, even less so ‘a series of states’. The constitution of series itself is a problematic enterprise — which means it needs to attend to its own singularities, and go through a process of progressive determination of a problem. This progressive determination means that as dimensions or series become more and more articulated, our ability to express the thought that grasps at a problem gets pressed down certain discursive lines. But a well determined concept like ‘state’ or ‘heat’ or so on must differentiate itself from within a manifold initially — there’s many fateful events in this process, which forms the history of our knowledge and the shifting a priori of our thought, and the sense of our questions. But the events, the singularities, and the problems that generate them always outstrip the sense of our questions, the dimensions we trace to ensnare them, the series we specify as the themes of the principal development of things. We always encounter something immeasurably complex, and even monstrous, something impossible to fully grasp but nonetheless realized in the most obvious and apparent ways before us.
One final, and crucial caveat is that we need to remember that if the problematic is seen as metaphysically or ontologically ‘prior’ to things, it’s not the case that there is a pot of water, which we analyse down certain dimensions, discovering singularities and events, but, rather, that we can denote an individuated object is a product of these series producing singularities that resonate within a ‘vicinity’. Individuated entities, pots as well as people, have as their ground a pre-individual, problematic, n-dimensional field.
Works Cited
Bowden, S. (2011). The Priority of Events: Deleuze’s Logic of Sense. Edinburgh: Edinburgh University Press.
Deleuze, G., Lester, M., Stivale, C. and Boundas, C. (1990). The Logic of Sense. London: Athlone.
Deleuze, G., Patton, P. (2011) Difference and Repetition. London: Continuum.
Sartre, J. (2008) Being and Nothingness. Oxford: Routledge Classics.
Smith, D. (2006) Axiomatics and problematics as two modes of formalisation: Deleuze’ epistemology of mathematics. In S. Duffy, ed., Virtual Mathematics: The Logic of Difference. Manchester: Clinamen Press.
Voss, D. (2013). Deleuze’s Rethinking of the Notion of Sense. Deleuze Studies, 7(1), pp.1–25.
Williams, J. (2008). Gilles Deleuze’s Logic of Sense: A critical introduction and guide. Edinburgh: Edinburgh University Press.